浮點數陷阱 IEEE 754 誤差

浮點數不只是你想像的小數點

陳乾正 2017/12/25 01:58:48

1 20348

浮點數不只是你想像的小數點

簡介	在程式設計的領域裡將近二十年的時光，不時就會看到不論是剛投入程式設計的新手，抑是己經撰寫程式己有多年經驗的資深工程師，習慣遇到需要使用小數運算時就使用double處理，今天我們就來深入認識浮點數的虛實。
作者	陳乾正

或許，不論是在課堂上或是坊間的程式設計教學書籍只要談到浮點數double、float型別，就一定是舉小數點值運算、印出的範例，然後就介紹到此打住沒有再探討，所以讓大部份的人在腦海裡印下小數值運算就是用double型別變數來存放處理，也因此埋下了一些地雷等著那天時機成熟爆炸，經驗了一段鬼打牆才真的認識了浮點數是怎麼回事。

只要看到有工程師使用浮點數型別，心裡難免要犯嘀咕一下，我們是開發商業金融系統啊，真的用不到浮點數！！每每在專案的中後期，總不免要掃一下程式碼看看是否有那裡使用了浮點數型別有沒有問題才安心。

為什麼不用浮點數呢？我們來看一下c#中double的運算判斷

double num = 0.1;

Console.WriteLine(String.Format("(0.1 等於 0.1) ==> {0}, 值為{1:R}", num == 0.1, num));

Console.WriteLine("");

double num1 = 0;

double[] nums = new double[] { 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 };

for (int i = 0; i < 10; i++)

{

num1 = num1 + 0.1;

Console.WriteLine(String.Format("(0.1累加{0}次等於{1}) ==> {2}, 值為{3:R}", i + 1, nums[i], num1 == nums[i], num1));

}

Console.WriteLine("");

double num2 = num * 0.1 * 10;

Console.WriteLine(String.Format("(0.1 * 0.1 * 10 等於 0.1) ==> {0}, 值為{1:R}", num2 == 0.1, num2));

執行結果如下，一般第一次看到應該都會懷疑這不會C#的Bug吧。

那再來看看javascript，我們都知道javascript是弱型別，對於數值的處理不管整數或是有小數，都只有一種型別Number，而且Number是實作64位元的雙精浮點數(double)型別。

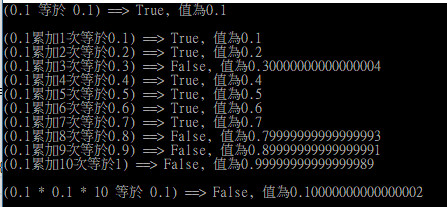
var num = 0.1;

document.write('(0.1等於0.1) ==> ' + (num == 0.1).toString() + ', 值為' + num.toFixed(20) + ' ');

var num1 = 0;

var nums = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0];

for(i = 0; i < 10; i++) {

num1 = num1 + 0.1;

document.write('(0.1累加' + (i+1) + '次等於' + nums[i] + ') ==> ' + (num1 == nums[i]).toString() + ', 值為' + num1.toFixed(20) + ' ');

}

document.write(' ');

var num2 = num * 0.1 * 10;

document.write('(0.1 * 0.1 * 10 等於 0.1) ==> ' + (num2 == 0.1).toString() + ', 值為' + num2.toFixed(20) + ' ');

結果似乎是一樣的，該不會連Javascript也一樣有Bug吧！！！

其實，浮點數型別的用途並不是只是一個跑龍套的小弟，用來處理小數點這點簡單運算，在科學、工程、統計…等等領域都少不了浮點數的運用，我們來看一下C#中浮點數的定義

https://docs.microsoft.com/zh-tw/dotnet/csharp/language-reference/keywords/double

浮點運算式可以接受實數值，包含下列值的集合：

• 正零和負零。
• 正無限大和負無限大。
• 非數字值 (NaN) 。
• 非零值的有限集合。

有關實數可參考維基百科https://zh.wikipedia.org/wiki/%E5%AE%9E%E6%95%B0

在實際的世界中實數會有無理數，也就是無限循環小數的值，例如：

圓周率π = 3. 141592653589793238462643383279…

常數e = 2.71828182845904523536…

2的平方根 = 1.4142135623730950488016887242…

在電腦的世界裡，資料的處理與儲存最小單位是二進位位元，以位元並無法真正的表達一個無理數值，會造成二個結果，一是輸入儲存的值不一定精確，二是運算計算後的結果值會有尾數誤差，有些人把這個結果稱為浮點數的陷阱，但其實是我們對浮點數型別的不瞭解所造成，在C#中浮點數類型如下，以double為例，雖然最小可以表示至小數點以下324位小數或是最大至308位數字，但其實只有最前15或16位數字是精確的，其他以下部份都會是不精確的值。

類型	大概範圍	精確度
float	±1.5e−45 至 ±3.4e38	7 位數
double	±5.0e−324 至 ±1.7e308	15-16 位數

現今軟硬體中浮點數處理大部份都是依循IEEE 754二進位浮點數算術標準來設計，IEEE 754將記錄浮點數值分成符號、指數及有效數值三個部份構成，以C# double為例，64個位元切割部位如下：

63	52~62	0~51
符號位	指數偏移值	有效數值

• 符號位：以1個位元表示浮點數值為正或負。

• 指數偏移值：以11個位元存放浮點數正規化後的指數值加上127，指數值為2的次方。

• 有效數值：以52個位元存放，即是將浮點數值二進位規化做整數最小數值後表示。

例如22.75轉換二進位表示為10110.11，做浮點數正規化後為1.011011，指數為2的4次方，故存放指數偏移值為4+127=131，並將正規化後的值1.011011去掉整數1後的011011存放至有效數值，而浮點數的表示法為2.275E+1。

但有些情況某些十進位小數是無法正確轉換為二進位的，例如0.3會是0.010011001…的循環小數，因此在轉換存放再轉回浮點數值時就產生了誤差。

IEEE 754詳細資訊請參考維基百科https://zh.wikipedia.org/wiki/IEEE_754

既然浮點數會有誤差不精確情況，那我們要怎麼處理小數運算呢? 在C#可以使用decimal型別，精確度高非常適合用做財務和金融計算，在javascript沒有選擇，最好的方式就是在適當的地方，例如連乘除的過程或最後取值時將計算值做四拾五入到某一小數位數，例如第二位小數或整數。

最後還是強調，浮點數型別不是不能用，而是要用在適當的地方及小心處理，若需要做小數的運算判斷則儘量避免使用浮點數型別。

關於C#浮點數型別的更詳細資訊可參考https://docs.microsoft.com/zh-tw/dotnet/api/system.double?view=netframework-4.7.1

陳乾正

.NetCore 使用StyleCop.Analyzers管理程式碼

Blazor WebAssembly 載入優化

利用Fido2NetLib，完成WebAuthn登入，實現無密碼登入讓帳號變得更安全

C# 使用 SSH.NET SFTP 上傳及下載範例

自訂Swagger Request Header

Create a Windows Service in .NET Core