List與Dictionary時間複雜度比較

1. 前言：

今天帶大家來探討到底List跟Dictionary在實際從集合找出自已需要的資料，到底在資料量大時，搜尋時間所花的差別性

2. 時間複雜度說明：

在程式設計中，決定某程式區段的步驟計數是程式設計師在控制整體程式系統時間的重要因素，不過要決定精確的次數卻也真是一困難的工作。特別是在不確定型(如指令x=l和x=x2+x3.15/x-4)比較，雖然我們都將其視為一個指令，不過運用的複雜程度理所當然影響了真正精確的執行時間。由此得知花費很大的功夫去計算真正的執行次數是沒有意義的。所以我們往往以一種「概量」的精神來做為衡量的準則，稱為「時間複雜度」(Time complexity)。按著我們就來看它的詳細介紹:

我們定義一個T(n)，表示在一個完全理想狀態的計算機中程式所執行的實際指令次數。一個程式的執行時間並不完全和輸入量有關，演算法的好壞也會影響，所以我們可以把它當作輸入量為n的一種函數。又在此我們可以定義對輸入量n而言，它的最大執行時間就是時間複雜度(Time complexity)的衡量標準。通常在漸近表示法(Asymptotic Notation)中，我們一般以Big-oh來表示。

3. 常見的Big-oh：

對於比較2個不同的時間複雜度，千萬不可以用直觀的方法來判斷。例如有2種演算法，時間複雜度各為O(n)與O(n2)。如果這2種方法的實際執行次數T'(n)=2n，T"(n)=n2，則n>2時，2n<n2，對時間複雜度而言，O(n)優於O(n2)(所謂"優於"，就是所花的時間較少)。注意！當n≦2時2n≧n2，則O(n2)優於O(n)。由上面的說明，我們可以清楚知道時間複雜度事實上只表示實際次數的一個量度的層級，並不是真實的執行次數。此外，有關目前常見的Big-oh有下列幾種情形：

1.O(1)或O(c)：稱為常數時間(constant time)

　　這表示演算法則的執行時間是一個常數倍，而忽略資料集合大小的變化。一個例子是在電腦中它存取RAM所花的時間，在記憶體中去讀取及寫入所用的時間是相同的，而不考慮整個記憶體的數量。如果有這樣的演算法則存在，則我們可以在任何大小的資料集合中自由的使用，而不需要擔心時間或運算的次數會一直成長或變得很高。

2. O(n)：稱為線性時間(linear time)

　　它執行的時間會隨資料集合的大小而線性成長。我們可以找到一個例子是在一個沒有排列過的資料集中要找一個最大元素，且我們以簡單的方式去解釋其內容，直到我們將所有的資料都找過並且找到最大值為止。

3.O(log2n)：稱為次線性時間(sub-linear time)

　　這一種函式的成長速度比線性的程序還慢，而此常數(它是不成長的)的情形還快。

4.O(n2)：稱為平方時間(quadratic time)

　　演算法則執行時間會成二次方的成長，這種會變得不切實際，特別是當資料集合的大小變得很大時。

5.O(n3)：稱為立方時間(cubic time)

6.O(2n)：稱為指數時間(exponential time)

7.O(n1og2n)

4. 實作驗證：

10000筆資料比較

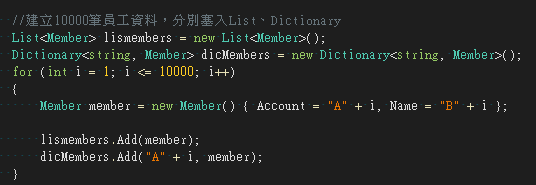
1000000筆資料比較

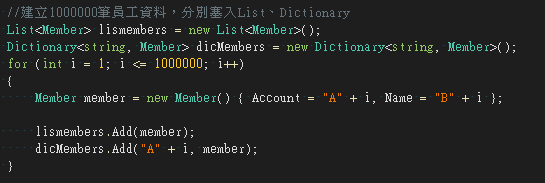
5. 總結：

當搜尋的資料集合越大時，不妨可以考慮使用Dictionary來試試，或許可以更進一步提升搜尋的效能。

6. 參考網址：

https://market.cloud.edu.tw/content/senior/computer/ks_ks/book/algodata/algorithm/algo5.htm